Álgebra relacional
Describe el aspecto de la manipulación de datos. Estas operaciones se usan como una representación intermedia de una consulta a una base de datos y, debido a sus propiedades algebraicas, sirven para obtener una versión más optimizada y eficiente de dicha consulta.
Las operaciones
Una condición puede ser una combinación booleana, donde se pueden usar operadores como: ,
,  , combinándolos con operadores
, combinándolos con operadores  .
.
 son atributos de la relación R .
son atributos de la relación R .
Ejemplo:
Ejemplo:
Estas operaciones son fundamentales en el sentido en que (1) todas las demás operaciones pueden ser expresadas como una combinación de éstas y (2) ninguna de estas operaciones pueden ser omitidas sin que con ello se pierda información.
Unión natural (
La operación unión natural en el álgebra relacional es la que permite reconstruir las tablas originales previas al proceso de normalización. Consiste en combinar las proyección, selección y producto cartesiano en una sola operación, donde la condición  es la igualdad Clave Primaria = Clave Externa (o Foranea), y la proyección elimina la columna duplicada (clave externa).
es la igualdad Clave Primaria = Clave Externa (o Foranea), y la proyección elimina la columna duplicada (clave externa).
Expresada en las operaciones básicas, queda
Una reunión theta ( θ-Join) de dos relaciones es equivalente a:
 es libre.
es libre.
Si la condición es una igualdad se denomina EquiJoin.
es una igualdad se denomina EquiJoin.
El operador división A / B retorna todos los distintos valores de x tales que para todo valor y en B existe una tupla en A.
en A.
Por ejemplo: Ģ sum(puntos) as Total Equipo (PARTIDOS).
Ejemplos!
Mostrar los nombres de los alumnos y su apoderado
Primero, realizaremos una combinación entre alumnos y apoderados (pues necesitamos saber a que alumno le corresponde tal apoderado). La combinación realizará un producto cartesiano, es decir, para cada tupla de alumnos (todas las filas de alumnos) hará una mezcla con cada una tupla de apoderados y seleccionará aquellas nuevas tuplas en que alumnos.id sea igual a apoderados.id_alumno, esto es:
Las operaciones
Básicas
Cada operador del álgebra acepta una o dos relaciones y retorna una relación como resultado. σ y Π son operadores unarios, el resto de los operadores son binarios. Las operaciones básicas del álgebra relacional son:Seleccióna (σ)
Permite seleccionar un subconjunto de tuplas de una relación (R), todas aquellas que cumplan la(s) condición(es) P, esto es:Una condición puede ser una combinación booleana, donde se pueden usar operadores como:
 ,
,  , combinándolos con operadores
, combinándolos con operadores  .
.Proyección (Π)
Permite extraer columnas (atributos) de una relación, dando como resultado un subconjunto vertical de atributos de la relación, esto es: son atributos de la relación R .
son atributos de la relación R .Ejemplo:
Producto cartesiano (x)
El producto cartesiano de dos relaciones se escribe como:Ejemplo:
Unión (∪)
La operaciónDiferencia (-)
La diferencia de dos relaciones, R y S denotada por:Estas operaciones son fundamentales en el sentido en que (1) todas las demás operaciones pueden ser expresadas como una combinación de éstas y (2) ninguna de estas operaciones pueden ser omitidas sin que con ello se pierda información.
No básicas o Derivadas
Entre los operadores no básicos tenemos:Intersección (∩)
La intersección de dos relaciones se puede especificar en función de otros operadores básicos:
Unión natural (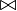 ) (Natural Join)
) (Natural Join)
La operación unión natural en el álgebra relacional es la que permite reconstruir las tablas originales previas al proceso de normalización. Consiste en combinar las proyección, selección y producto cartesiano en una sola operación, donde la condición  es la igualdad Clave Primaria = Clave Externa (o Foranea), y la proyección elimina la columna duplicada (clave externa).
es la igualdad Clave Primaria = Clave Externa (o Foranea), y la proyección elimina la columna duplicada (clave externa).Expresada en las operaciones básicas, queda
Una reunión theta ( θ-Join) de dos relaciones es equivalente a:
 es libre.
es libre.Si la condición
 es una igualdad se denomina EquiJoin.
es una igualdad se denomina EquiJoin.División (/)
Supongamos que tenemos dos relaciones A(x, y) y B(y) donde el dominio de y en A y B, es el mismo.El operador división A / B retorna todos los distintos valores de x tales que para todo valor y en B existe una tupla
 en A.
en A.Agrupación (Ģ)
Permite agrupar conjuntos de valores en función de un campo determinado y hacer operaciones con otros campos.Por ejemplo: Ģ sum(puntos) as Total Equipo (PARTIDOS).
Ejemplos!
| ID | NOMBRE | CIUDAD | EDAD |
| 01 | Pedro | Bogota | 14 |
| 11 | Juan | Cali | 18 |
| 21 | Diego | Cartagena | 12 |
| 31 | Rosita | Medellin | 15 |
| 41 | Manuel | Cartagena | 17 |
| ID | NOMBRE | FONO | ID_ALUMNO |
| 054 | Víctor | 654644 | 21 |
| 457 | José | 454654 | 11 |
| 354 | María | 997455 | 31 |
| 444 | Paz | 747423 | 01 |
| COD | NOMBRE | FECHA_INICIO | DURACION | VALOR |
| 01142 | Sicología | 13-01 | 15 | 3.000 |
| 02145 | Biología | 15-02 | 12 | 2.500 |
| 03547 | Matemáticas | 01-03 | 30 | 4.000 |
| 04578 | Música | 05-04 | 10 | 1.500 |
| 05478 | Física | 20-04 | 15 | 3.200 |
| ID | ID_AL | COD |
| 1 | 01 | 05478 |
| 2 | 01 | 02145 |
| 3 | 11 | 03547 |
| 4 | 21 | 02145 |
| 5 | 41 | 03547 |
Mostrar los nombres de los alumnos y su apoderado
Primero, realizaremos una combinación entre alumnos y apoderados (pues necesitamos saber a que alumno le corresponde tal apoderado). La combinación realizará un producto cartesiano, es decir, para cada tupla de alumnos (todas las filas de alumnos) hará una mezcla con cada una tupla de apoderados y seleccionará aquellas nuevas tuplas en que alumnos.id sea igual a apoderados.id_alumno, esto es:
| ID (alumno) | NOMBRE (alumno) | CIUDAD | EDAD | ID (apoderado) | NOMBRE (apoderado) | FONO | ID_ALUMNO |
| 01 | Pedro | Santiago | 14 | 054 | Víctor | 654644 | 21 |
| 01 | Pedro | Santiago | 14 | 457 | José | 454654 | 11 |
| 01 | Pedro | Santiago | 14 | 354 | María | 997455 | 31 |
| 01 | Pedro | Santiago | 14 | 444 | Paz | 747423 | 01 |
| 11 | Juan | Buenos Aires | 18 | 054 | Víctor | 654644 | 21 |
| 11 | Juan | Buenos Aires | 18 | 457 | José | 454654 | 11 |
| 11 | Juan | Buenos Aires | 18 | 354 | María | 997455 | 31 |
| 11 | Juan | Buenos Aires | 18 | 444 | Paz | 747423 | 01 |
| 21 | Diego | Lima | 12 | 054 | Víctor | 654644 | 21 |
| 21 | Diego | Lima | 12 | 457 | José | 454654 | 11 |
| 21 | Diego | Lima | 12 | 354 | María | 997455 | 31 |
| 21 | Diego | Lima | 12 | 444 | Paz | 747423 | 01 |
| 31 | Rosita | Concepción | 15 | 054 | Víctor | 654644 | 21 |
| 31 | Rosita | Concepción | 15 | 457 | José | 454654 | 11 |
| 31 | Rosita | Concepción | 15 | 354 | María | 997455 | 31 |
| 31 | Rosita | Concepción | 15 | 444 | Paz | 747423 | 01 |
| 41 | Manuel | Lima | 17 | 054 | Víctor | 654644 | 21 |
| 41 | Manuel | Lima | 17 | 457 | José | 454654 | 11 |
| 41 | Manuel | Lima | 17 | 354 | María | 997455 | 31 |
| 41 | Manuel | Lima | 17 | 444 | Paz | 747423 | 01 |
Analizador sintáctico
Un analizador sintáctico (en inglés parser) es una de las partes de un compilador que transforma su entrada en un árbol de derivación.
El análisis sintáctico convierte el texto de entrada en otras estructuras (comúnmente árboles), que son más útiles para el posterior análisis y capturan la jerarquía implícita de la entrada. Un analizador léxico crea tokens de una secuencia de caracteres de entrada y son estos tokens los que son procesados por el analizador sintáctico para construir la estructura de datos, por ejemplo un árbol de análisis o árboles de sintaxis abstracta.
El análisis sintáctico también es un estado inicial del análisis de frases de lenguaje natural. Es usado para generar diagramas de lenguajes que usan flexión gramatical, como los idiomas romances o el latín. Los lenguajes habitualmente reconocidos por los analizadores sintácticos son los lenguajes libres de contexto. Cabe notar que existe una justificación formal que establece que los lenguajes libres de contexto son aquellos reconocibles por un autómata de pila, de modo que todo analizador sintáctico que reconozca un lenguaje libre de contexto es equivalente en capacidad computacional a un autómata de pila.
Los analizadores sintácticos fueron extensivamente estudiados durante los años 70 del siglo XX, detectándose numerosos patrones de funcionamiento en ellos, cosa que permitió la creación de programas generadores de analizadores sintáticos a partir de una especificación de la sintaxis del lenguaje en forma Backus-Naur por ejemplo, tales como yacc, GNU bison y javaCC.
El análisis sintáctico también es un estado inicial del análisis de frases de lenguaje natural. Es usado para generar diagramas de lenguajes que usan flexión gramatical, como los idiomas romances o el latín. Los lenguajes habitualmente reconocidos por los analizadores sintácticos son los lenguajes libres de contexto. Cabe notar que existe una justificación formal que establece que los lenguajes libres de contexto son aquellos reconocibles por un autómata de pila, de modo que todo analizador sintáctico que reconozca un lenguaje libre de contexto es equivalente en capacidad computacional a un autómata de pila.
Los analizadores sintácticos fueron extensivamente estudiados durante los años 70 del siglo XX, detectándose numerosos patrones de funcionamiento en ellos, cosa que permitió la creación de programas generadores de analizadores sintáticos a partir de una especificación de la sintaxis del lenguaje en forma Backus-Naur por ejemplo, tales como yacc, GNU bison y javaCC.
Heurística (informática)
En computación, dos objetivos fundamentales son encontrar algoritmos con buenos tiempos de ejecución y buenas soluciones, usualmente las óptimas. Una heurística es un algoritmo que abandona uno o ambos objetivos; por ejemplo, normalmente encuentran buenas soluciones, aunque no hay pruebas de que la solución no pueda ser arbitrariamente errónea en algunos casos; o se ejecuta razonablemente rápido, aunque no existe tampoco prueba de que siempre será así. Las heurísticas generalmente son usadas cuando no existe una solución óptima bajo las restricciones dadas (tiempo, espacio, etc.), o cuando no existe del todo.
A menudo, pueden encontrarse instancias concretas del problema donde la heurística producirá resultados muy malos o se ejecutará muy lentamente. Aun así, estas instancias concretas pueden ser ignoradas porque no deberían ocurrir nunca en la práctica por ser de origen teórico. Por tanto, el uso de heurísticas es muy común en el mundo real.
Objetivos de los sistemas de bases de datos
Corregir anomalías en el acceso concurrente: Para mejorar el funcionamiento del sistema y tener un tiempo de respuesta más corto, muchos sistemas permiten que varios usuarios actualicen la información simultáneamente. En un ambiente de este tipo, la interacción de las actualizaciones concurrentes puede resultar en información inconsistente. Para prevenir estas situaciones debe mantenerse alguna forma de supervisión en el sistema.
Arboles de consultas
Una base de datos es accesada de esta manera la técnica que se utiliza es la de fragmentación de datos que puede ser hibrida, horizontal y vertical.
A menudo, pueden encontrarse instancias concretas del problema donde la heurística producirá resultados muy malos o se ejecutará muy lentamente. Aun así, estas instancias concretas pueden ser ignoradas porque no deberían ocurrir nunca en la práctica por ser de origen teórico. Por tanto, el uso de heurísticas es muy común en el mundo real.
Objetivos de los sistemas de bases de datos
Corregir anomalías en el acceso concurrente: Para mejorar el funcionamiento del sistema y tener un tiempo de respuesta más corto, muchos sistemas permiten que varios usuarios actualicen la información simultáneamente. En un ambiente de este tipo, la interacción de las actualizaciones concurrentes puede resultar en información inconsistente. Para prevenir estas situaciones debe mantenerse alguna forma de supervisión en el sistema.
Arboles de consultas
Transformaciones equivalentes
1.-el servidor recive una peticion de un nodo
2.-el servidor es atacado por el acceso concurrente a la base de datos cargada localmente
3.-el servidor muestra un resultado y le da un hilo a cada una de las maquinas nodo de la red local.
Una base de datos es accesada de esta manera la técnica que se utiliza es la de fragmentación de datos que puede ser hibrida, horizontal y vertical.
En esta fragmentación lo que no se quiere es perder la consistencia de los datos, por lo tanto se respetan las formas normales de la base de datos ok.
Bueno para realizar una transformación en la consulta primero desfragmentamos siguiendo los estandares marcados por las reglas formales y posteriormente realizamos el envio y la maquina que recibe es la que muestra el resultado pertinente para el usuario, de esta se puede producir una copia que sera la equivalente a la original.





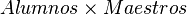

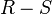

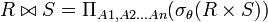


No hay comentarios:
Publicar un comentario